モード分解の数値例
前準備
\(\boldsymbol{M}\)を質量行列、\(\boldsymbol{C}\)を減衰行列、\(\boldsymbol{K}\)を剛性行列、\(\boldsymbol{x}\)を位置ベクトル、\(\boldsymbol{f}\)を外力ベクトルとしたとき多自由度振動系の運動方程式は次式のように表される。
\begin{align} \boldsymbol{M}\cfrac{d^2\boldsymbol{x}}{dt^2}+\boldsymbol{C}\cfrac{d\boldsymbol{x}}{dt}+\boldsymbol{K}\boldsymbol{x}=\boldsymbol{f} \end{align}
次式のような一般化固有値問題の解\(\boldsymbol{T}\)を求める。
\begin{align} \boldsymbol{M}\boldsymbol{T}\boldsymbol{\Omega}^2=\boldsymbol{K}\boldsymbol{T}\end{align}
変換行列\(\boldsymbol{T}\)と変位ベクトルを\(\boldsymbol{x}=\boldsymbol{T}\boldsymbol{\phi}\)のように変換すると、以下のようにモード分解された運動方程式が得られる。
\begin{align} \boldsymbol{T}^\textrm{T}\boldsymbol{M}\boldsymbol{T}\cfrac{d^2\boldsymbol{\phi}}{dt^2}+\boldsymbol{T}^\textrm{T}\boldsymbol{C}\boldsymbol{T}\cfrac{d\boldsymbol{\phi}}{dt}+\boldsymbol{T}^\textrm{T}\boldsymbol{K}\boldsymbol{T}\boldsymbol{\phi}=\boldsymbol{T}^\textrm{T}\boldsymbol{f}\\\boldsymbol{\bar{M}}\cfrac{d^2\boldsymbol{\phi}}{dt^2}+\boldsymbol{\bar{C}}\cfrac{d\boldsymbol{\phi}}{dt}+\boldsymbol{\bar{K}}\boldsymbol{\phi}=\boldsymbol{T}^\textrm{T}\boldsymbol{f}\\\cfrac{d^2\boldsymbol{\phi}}{dt^2}+\boldsymbol{\bar{M}}^{-1}\boldsymbol{\bar{C}}\cfrac{d\boldsymbol{\phi}}{dt}+\boldsymbol{\Omega}^2\boldsymbol{\phi}=\boldsymbol{\bar{M}}^{-1}\boldsymbol{T}^\textrm{T}\boldsymbol{f} \end{align}
上記のモード分解では\(\boldsymbol{\bar{M}}^{-1}\boldsymbol{\bar{C}}\)が対角行列になるとは限らない。しかし実用上は減衰が小さいため、\(\boldsymbol{\bar{M}}^{-1}\boldsymbol{\bar{C}}\)の非対角項を無視しても問題ないことが多い。
減衰が無視できないときはモード形式(Eigenstructure decomposition)を用いるとよい。モード形式を求めるために、まず次式で示すように運動方程式を状態方程式に変換する。
\begin{align} \left[\begin{array}{cc}\boldsymbol{I}&\boldsymbol{0}\\\boldsymbol{0}&\boldsymbol{M}\end{array}\right]\cfrac{d}{dt}\left(\begin{array}{c}\boldsymbol{x}\\\boldsymbol{v}\end{array}\right)=\left[\begin{array}{cc}\boldsymbol{0}&\boldsymbol{I}\\-\boldsymbol{K}&-\boldsymbol{C}\end{array}\right]\left(\begin{array}{c}\boldsymbol{x}\\\boldsymbol{v}\end{array}\right)+\left(\begin{array}{c}\boldsymbol{0}\\\boldsymbol{f}\end{array}\right) \end{align}
次に、以下に示す一般化固有値問題の固有値\(\boldsymbol{\Lambda}\)と固有ベクトル行列\(\boldsymbol{V}\)を求める。
\begin{align} \left[\begin{array}{cc}\boldsymbol{I}&\boldsymbol{0}\\\boldsymbol{0}&\boldsymbol{M}\end{array}\right]\boldsymbol{V}\boldsymbol{\Lambda}=\left[\begin{array}{cc}\boldsymbol{0}&\boldsymbol{I}\\-\boldsymbol{K}&-\boldsymbol{C}\end{array}\right]\boldsymbol{V} \end{align}
実数な固有値に対応した固有ベクトルを\(\boldsymbol{v}_i^r\)、複素数な固有値に対応した固有ベクトルを\(\boldsymbol{v}_j^c\)としたとき、次の変換行列を考える。
\begin{align}&\boldsymbol{T}=\left[\boldsymbol{v}^r_1,\boldsymbol{v}^r_2,...,\textrm{Re}\left(\boldsymbol{v}^c_1\right),\textrm{Im}\left(\boldsymbol{v}^c_1\right),\textrm{Re}\left(\boldsymbol{v}^c_2\right),\textrm{Im}\left(\boldsymbol{v}^c_2\right),...\right]\\&\left(\begin{array}{c}\boldsymbol{x}\\\boldsymbol{v}\end{array}\right)=\boldsymbol{T}\left(\begin{array}{c}\boldsymbol{\phi}\\\boldsymbol{\psi}\end{array}\right)\end{align}
変換行列\(\boldsymbol{T}\)と状態ベクトル\(\boldsymbol{\phi}, \boldsymbol{\psi}\)を用いると状態方程式は次式のようになる。
\begin{align} \cfrac{d}{dt}\left(\begin{array}{c}\boldsymbol{\phi}\\\boldsymbol{\psi}\end{array}\right)&=\boldsymbol{T}^{-1}\left[\begin{array}{cc}\boldsymbol{0}&\boldsymbol{I}\\-\boldsymbol{M}^{-1}\boldsymbol{K}&-\boldsymbol{M}^{-1}\boldsymbol{C}\end{array}\right]\boldsymbol{T}\left(\begin{array}{c}\boldsymbol{\phi}\\\boldsymbol{\psi}\end{array}\right)+\boldsymbol{T}^{-1}\left(\begin{array}{c}\boldsymbol{0}\\\boldsymbol{M}^{-1}\boldsymbol{f}\end{array}\right)\\&=\left[\begin{array}{cc}\boldsymbol{\Lambda}&\boldsymbol{0}\\\boldsymbol{0}&\boldsymbol{D}\end{array}\right]\left(\begin{array}{c}\boldsymbol{\phi}\\\boldsymbol{\psi}\end{array}\right)+\left(\begin{array}{c}\boldsymbol{f}\\\boldsymbol{g}\end{array}\right) \end{align}
\begin{align} \boldsymbol{\Lambda}&=\textrm{diag}\left(\lambda_1,\lambda_2,...\right)\\\boldsymbol{D}&=\textrm{blkdiag}\left(\boldsymbol{D}_1,\boldsymbol{D}_2,...\right)\\\boldsymbol{D}_i&=\left[\begin{array}{cc}-\zeta_i\omega_i&\omega_i^d\\-\omega_i^d&-\zeta_i\omega_i\end{array}\right]\\\omega_i^d&=\omega_i\sqrt{1-\zeta_i^2} \end{align}
上記のように、元の運動方程式をモード減衰比\(\zeta_i\)とモード固有角周波数\(\omega_i\)に分解が可能である。
減衰が小さい場合の数値例
次のような運動方程式を考える。
\begin{align} \left[\begin{array}{cc}3&0\\0&2\end{array}\right]\cfrac{d^2}{dt^2}\left(\begin{array}{c}x_1\\x_2\end{array}\right)&+ \left[\begin{array}{cc}0.1&-0.2\\-0.2&0.5\end{array}\right]\cfrac{d}{dt}\left(\begin{array}{c}x_1\\x_2\end{array}\right)\\&+\left[\begin{array}{cc}30&-10\\-10&10\end{array}\right]\left(\begin{array}{c}x_1\\x_2\end{array}\right)=\left(\begin{array}{c}f\\0\end{array}\right) \end{align}
状態方程式で表記すると次式のようになる。
\begin{align} \left[\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&2\end{array}\right]\cfrac{d}{dt}\left(\begin{array}{c}x_1\\x_2\\v_1\\v_2\end{array}\right)= \left[\begin{array}{cccc}0&0&1&0\\0&0&0&1\\-30&10&-0.1&0.2\\10&-10&0.2&-5\end{array}\right]\left(\begin{array}{c}x_1\\x_2\\v_1\\v_2\end{array}\right)+\left(\begin{array}{c}0\\0\\f\\0\end{array}\right) \end{align}
モード分解
次式の一般化固有値問題の解\(\boldsymbol{T}\)を求める。固有値問題を解く際はOctaveを使用した。
\begin{align} \left[\begin{array}{cc}3&0\\0&2\end{array}\right]\boldsymbol{T}\boldsymbol{\Omega}^2=\left[\begin{array}{cc}30&-10\\-10&10\end{array}\right]\boldsymbol{T}\\\boldsymbol{T}=\left[\begin{array}{cc}-0.5037&-0.2822\\0.3456&-0.6169\end{array}\right]\\\boldsymbol{\Omega}^2=\left[\begin{array}{cc}12.2871&0\\0&2.7129\end{array}\right]\end{align}
上記変換行列を用いると、運動方程式は次式のようになる。なお、質量行列が単位行列となっており、この変換行列は正規化の特性も含まれている。
\begin{align} \cfrac{d^2\boldsymbol{\phi}}{dt^2}&+ \left[\begin{array}{cc}0.1547&-0.135\\-0.135&0.1286\end{array}\right]\cfrac{d\boldsymbol{\phi}}{dt}\\&+\left[\begin{array}{cc}12.29&0\\0&2.713\end{array}\right]\boldsymbol{\phi}=\left(\begin{array}{c}-0.5037\\-0.2822\end{array}\right)f\\\left(\begin{array}{c}x_1\\x_2\end{array}\right)&=\left[\begin{array}{cc}-0.5037&-0.2822\\0.3456&-0.6169\end{array}\right] \boldsymbol{\phi}\end{align}
完全にモードごとに分解するために、減衰項の非対角項(連成項)を0とする必要がある。連成項を0とすることで次式のように完全に分離が可能となる。
\begin{align} \cfrac{d^2\phi_1}{dt^2}+0.1547\cfrac{d\phi_1}{dt}+12.29\phi_1=-0.5037f\\\cfrac{d^2\phi_2}{dt^2}+0.1286\cfrac{d\phi_2}{dt}+2.713\phi_1=-0.2822f\\\left(\begin{array}{c}x_1\\x_2\end{array}\right)=\left[\begin{array}{cc}-0.5037&-0.2822\\0.3456&-0.6169\end{array}\right] \left(\begin{array}{c}\phi_1\\\phi_2\end{array}\right)\end{align}
この系のモード減衰比とモード固有角周波数は以下のようになる。
\begin{align} \zeta_1&=0.022069\\\zeta_2&=0.039042\\\omega_1&=3.5053\\\omega_2&=1.6471\end{align}
モード形式
次式の一般化固有値問題の解\(\boldsymbol{V}\)を求める。なお上付きバーは複素共役を表す。
\begin{align} \left[\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&3&0\\0&0&0&2\end{array}\right]\boldsymbol{V}\boldsymbol{\Lambda}&= \left[\begin{array}{cccc}0&0&1&0\\0&0&0&1\\-30&10&-0.1&0.2\\10&-10&0.2&-5\end{array}\right]\boldsymbol{V}\\\boldsymbol{V}&= \left[\begin{array}{cccc}\boldsymbol{v}_1&\boldsymbol{\bar{v}}_1&\boldsymbol{v}_2&\boldsymbol{\bar{v}}_2\end{array}\right]\\\boldsymbol{v}_1=\left(\begin{array}{c}-0.010955+0.28062i\\-0.014844-0.19252i\\0.98332+0.016677i\\-0.67287+0.066842i\end{array}\right)&, \boldsymbol{v}_2=\left(\begin{array}{c}0.0064523+0.27488i\\-0.018709-0.60148i\\0.45242-0.028338i\\-0.99207-0.0079267i\end{array}\right)\end{align}
次の変換行列\(\boldsymbol{T}\)を求める。
\begin{align} \boldsymbol{T}&= \left[\begin{array}{cccc}\textrm{Re}(\boldsymbol{v}_1)&\textrm{Im}(\boldsymbol{v}_1)&\textrm{Re}(\boldsymbol{v}_2)&\textrm{Im}(\boldsymbol{v}_2)\end{array}\right]\\&=\left[\begin{array}{cccc}-0.010955&0.28062&0.0064523&0.27488\\-0.014844&-0.19252&-0.018709&-0.60148\\0.98332&0.016677&0.45242&-0.028338\\-0.67287&0.066842&-0.99207&-0.0079267\end{array}\right]\end{align}
変換行列\(\boldsymbol{T}\)と状態ベクトル\(\boldsymbol{\phi}, \boldsymbol{\psi}\)を用いると状態方程式は次式のようになる。
\begin{align} \cfrac{d}{dt}\left(\begin{array}{c}\phi_1\\\phi_2\\\psi_1\\\psi_2\end{array}\right)=&\left[\begin{array}{cccc}-0.0772&-3.5011&0&0\\3.5011&-0.0772&0&0\\0&0&-0.0644&-1.6474\\0&0&1.6474&-0.0644\end{array}\right]\left(\begin{array}{c}\phi_1\\\phi_2\\\psi_1\\\psi_2\end{array}\right)\\&+\left(\begin{array}{c}0.2585\\-0.004226\\0.1757\\0.01049\end{array}\right)f\\\left(\begin{array}{c}x_1\\x_2\\v_1\\v_2\end{array}\right)=&\left[\begin{array}{cccc}-0.010955&0.28062&0.0064523&0.27488\\-0.014844&-0.19252&-0.018709&-0.60148\\0.98332&0.016677&0.45242&-0.028338\\-0.67287&0.066842&-0.99207&-0.0079267\end{array}\right]\left(\begin{array}{c}\phi_1\\\phi_2\\\psi_1\\\psi_2\end{array}\right)\end{align}
モード別に分けることで次式が得られる。
\begin{align} &\cfrac{d^2\phi_1}{dt^2}+0.1545\cfrac{d\phi_1}{dt}+12.26\phi_1=0.2585\cfrac{df}{dt}+0.03477f\\&\cfrac{d^2\phi_2}{dt^2}+0.1545\cfrac{d\phi_2}{dt}+12.26\phi_1=-0.004226\cfrac{df}{dt}+0.9048f\\&\cfrac{d^2\psi_1}{dt^2}+0.1288\cfrac{d\psi_1}{dt}+2.718\psi_1=0.1757\cfrac{df}{dt}-0.005967f\\&\cfrac{d^2\psi_2}{dt^2}+0.1288\cfrac{d\psi_2}{dt}+2.718\psi_1=0.01049\cfrac{df}{dt}+0.2901f\end{align}
この系のモード減衰比とモード固有角周波数は以下のようになる。
\begin{align} \zeta_1&=0.022059\\\zeta_2&=0.039074\\\omega_1&=3.5020\\\omega_2&=1.6486\end{align}
モード分解による式と比べ若干ずれていることが確認できる。
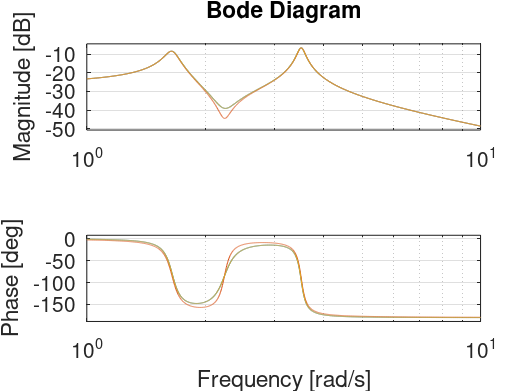
周波数特性
モード分解した場合とモード形式に変換した場合の周波数特性を図1に示します。赤で示したモード分解による特性が反共振の部分で若干ずれているがおおむね一致していることがわかる。また、モード形式は元のモデルに対して状態変数を変えただけなので、完全に一致している。
減衰が大きい場合の数値例
次に減衰が大きい場合の運動方程式を考える。先ほどの運動方程式に対して、減衰項が大きくなっていることがわかる。
\begin{align} \left[\begin{array}{cc}3&0\\0&2\end{array}\right]\cfrac{d^2}{dt^2}\left(\begin{array}{c}x_1\\x_2\end{array}\right)&+ \left[\begin{array}{cc}0.5&-1\\-1&25\end{array}\right]\cfrac{d}{dt}\left(\begin{array}{c}x_1\\x_2\end{array}\right)\\&+\left[\begin{array}{cc}30&-10\\-10&10\end{array}\right]\left(\begin{array}{c}x_1\\x_2\end{array}\right)=\left(\begin{array}{c}f\\0\end{array}\right) \end{align}
モード分解
先ほどと同様の手順で同時対角化を行うと次式が得られる。質量行列と剛性行列が先ほどと同じであるため、この時変換行列は先ほどと同じものになる。
\begin{align} \cfrac{d^2\boldsymbol{\phi}}{dt^2}&+ \left[\begin{array}{cc}3.461&-5.472\\-5.472&9.206\end{array}\right]\cfrac{d\boldsymbol{\phi}}{dt}\\&+\left[\begin{array}{cc}12.29&0\\0&2.713\end{array}\right]\boldsymbol{\phi}=\left(\begin{array}{c}-0.5037\\-0.2822\end{array}\right)f\\\left(\begin{array}{c}x_1\\x_2\end{array}\right)&=\left[\begin{array}{cc}-0.5037&-0.2822\\0.3456&-0.6169\end{array}\right] \boldsymbol{\phi}\end{align}
モード形式
こちらも同様の手順で同時対角化を行うと次式が得られる。最終的な状態方程式のみ示す。
\begin{align} \cfrac{d}{dt}\left(\begin{array}{c}\phi_1\\\phi_2\\\psi_1\\\psi_2\end{array}\right)=&\left[\begin{array}{cccc}-12.09&0&0&0\\0&-0.2808&0&0\\0&0&-0.1496&-3.131\\0&0&3.131&-0.1496\end{array}\right]\left(\begin{array}{c}\phi_1\\\phi_2\\\psi_1\\\psi_2\end{array}\right)\\&+\left(\begin{array}{c}0.002338\\0.01398\\-0.3348\\-0.001632\end{array}\right)f\end{align}
上式より、減衰が大きいため実数の固有値が得られたことから、この系の振動モードは1つのみであることがわかる。
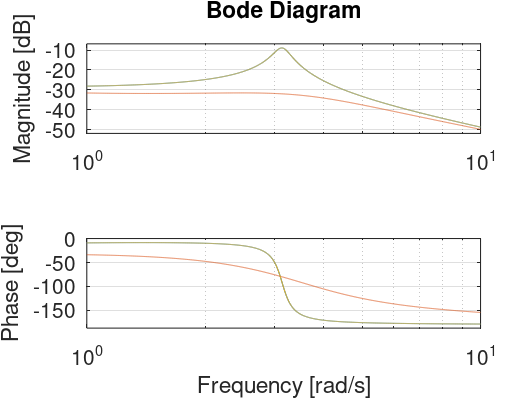
周波数特性
先ほどと同様に周波数特性(図2)を観察すると、赤で示したモード分解による特性には全く振動的な応答が得られなくて、うまくモード分解ができていないことが確認できる。
まとめ
減衰が小さい場合にはモード分解で充分にシステムの挙動を再現することが可能であるが、減衰が大きい場合ではモード分解は全く適切ではない。モード分解した際に計算されるモード減衰比が1に近い、1より大きい場合には再考する必要があることに注意せよ。